从电容谈起
还记得中学物理中学过的电容不,有的会想起C这个符号,有的会记起阻直流通交流,那我们从电容器最基本的定义开始:电容是指物体容纳电荷的能力,简单点说就是,能储存多少电荷量,可以把电容器想象成一个储存电荷的一个大池子,电荷可以通过导线不停地流入或者流出这个池子,池子越大,那储存的电荷量也就越多,也就意味着电容越大,如果1所示。

图1.电容与水池对比图
电荷在电容里累积的电荷量为Q(假设电容初始电荷为0),累积的电荷在电容两端产生电势差称为电容电压U,U与Q的关系是一个比例关系C(就是电容值)。如果简单理解的话,Is电流源相当于水泵,Q相当于池子的水量,U相当于水深,当水深U一定的时候,容纳的水量越多,说明池子越大,也就是意味着电容值C越大。I电流就相当于水管里的流速,I越大,说明往池子里充水速度越快,这就是Q变化率越快。于是把刚刚这段话变成公式,我们得到下面的式子:

其中:Q对应电荷量,U对应电容电压,I对应电流。
在这里电流源Is给电容C充电的电路里,如果一切条件理想化,那电容上的电压U会一直上升到无穷大,电容越大上升的速度越慢,Is越大,上升的速度越快。
RC与微分方程
如果我们将电流源Is变为电压源Us,同时在回路里加入一个电阻R,如图2所示,现在想问一下,电容C上的电压会怎么变化呢??
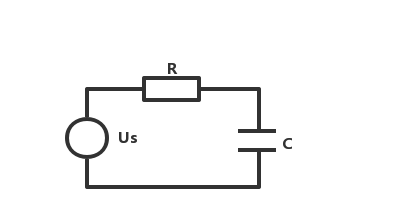
图2.RC充电电路
我们一步步来思考这个问题,首先,如果R为0的话,那会怎么样?电压源与电容并联,那电容会瞬间从0充满电压Us。下面加入电阻R,刚开始电容上电压为0,整个回路的充电电流就是Us/R,随着电容的电压Uc升高,这个充电电流会慢慢变小(Us-Uc)/R,也就是说随着电容电压的升高,充电的速度会越来越慢,最终稳定在Us电压,如果手动画一下的话,那大概走势如图3所示。是不是很像指数函数的变化,那我们就开始一步步分析吧。
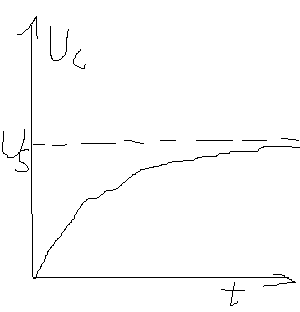
图3.电容电压变化图
如果用数学去表达刚刚描述这个动态过程的变化,该怎么做呢??首先电源电压等于电阻上的电压加上电容电压,然后电阻上的电流等于电容的电流,电容上的电流等于电容电压的变化率与电容之积,将这几句话用数学表达一下就是下面的数学公式。

有没有发现呀???微分方程出来了,对应一个RC电路。关于微分方程的求解,高等数学里专门写了一章去求微分方程的解,总之噼里啪啦一大堆,最后做题的时候,一顿代公式,什么齐次非齐次通解之类的,甚是烦恼,最后终于算出下面的解来:
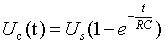
玩电子,怎么可能会被数学搞爬下,有没有什么好方法去简化这个求解过程呢,当然有啦,工程师更多是靠直觉,而非复杂计算。
电容Uc最终的稳态电压是Us,Uc的动态变化趋势,R变大那阻碍能力更强,Uc会变慢,C变大的话那意味着池子会变得更大,这个Uc也会变慢,这里就存在一个时间常数跟R和C都相关,对于任何一阶RC电路我们计算出RC这个时间常数,就可以预估系统的变化趋势,具体是怎样做呢??我们下面就开始用Simulink仿真玩。
设定:Us=1V,R=1k欧,C=1uF,Uc初始电压=0,Uc电压的动态变化过程如图3所示,这里RC= 1ms,这个称为时间常数,1倍时间常数Uc达到0.6513Us,2倍时间常数到0.8784Us,3倍时间常数到0.9576Us,4倍时间常数到0.9852Us。
大多数电子工程师不会去记那些微分方程的求解,而是记住这几个典型的数值,比如1倍时间常数到达稳态值的65%左右。
这就是工程师和数学家的区别,那有的同学可能会问,既然那些公式没啥用,那要他们干什么,这个不要急,形式化的公式会让计算机帮助我们去做仿真计算,下面我们就来介绍。
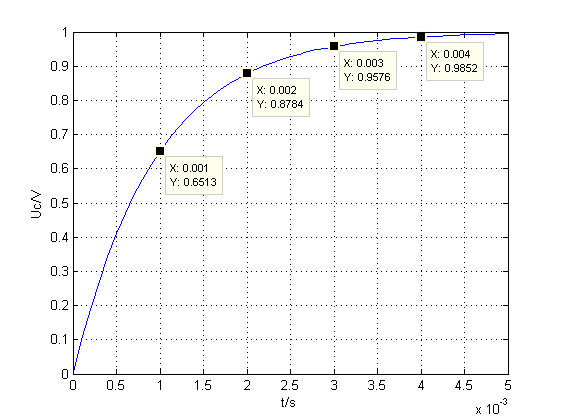
图3.RC动态过程
RC与差分方程
RC一阶电路,我们在计算机里如何仿真???

Uc的导数,还记不记得,我们高等数学里是怎么算的???
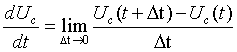
在高等数学里,利用极限来得到导数,当我们用计算机仿真的时候,是反向来用把导数离散化,这样我们就可以把第一个式子离散化为下式
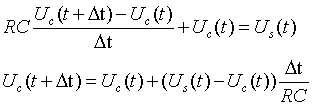
看到上面的式子了不,里面我们知道t时刻Uc的值,就可以通过t时刻的值,去计算t+deltaT时候的Uc值,这就是差分仿真模型。
于是根据上面的式子,我们就可以用matlab写代码仿真RC电路的动态过程,如图4所示。
R=1e3;%1000欧
C=1e-6;%1uF
dt=100e-6;%delta T 时间
T=5e-3;%仿真时间长度
t=0:dt:T;%时间轴
Us=ones(length(t),1);%1V
Uc=zeros(length(t),1);
for k=1:1:length(t)-1
Uc(k+1)=Uc(k)+(Us(k)-Uc(k))*dt/(R*C);
end
plot(t,Uc)
grid on
xlabel('t/s')
ylabel('Uc/V')
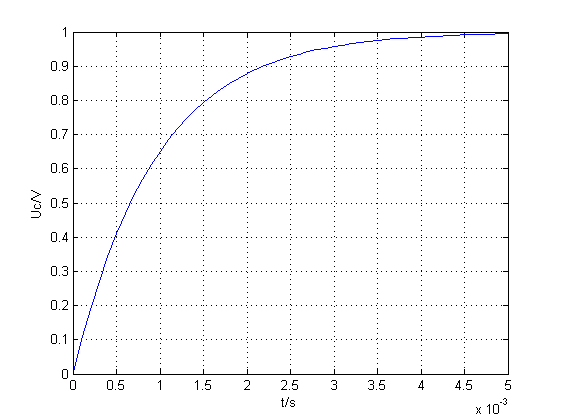
图4.RC电路动态仿真图
刚刚离散化的方程就是差分方程,整个计算机仿真动态系统都是基于这个差分方程来做的,如果想仿真精确一点,把仿真步长dt减小一点,但是意味着仿真时间会加长,如果想仿真快点,那就将dt设置长一些。
不管多么复杂的电路,都可以这样仿真,整个Simulink的底层仿真机制,也是这样玩的,都是基于差分方程做,分定步长和变步长两种玩法。
总结
我们用RC电路把最基本的微分方程求解,RC电路的动态响应,仿真过程,都进行了简单的汇总,如果条件允许的话,大家可以用真实的电阻和电容进行测试,并用示波器观察,会更有意思。我们这里的Us一直是恒定值,如果我们将Us改为动态变化的信号,会发生什么反应呢???敬请看下一节,我们将看到复数的出现,以此简化我们的计算。